COVID-19: The Search for Superspreaders
Note: This is an automated translation (using DeepL) of the original german article.
New simulation results reveal: If we use the right strategy, it is not bad news that a high percentage of new infections are caused by superspreaders.
Testing, tracing, isolating (TTI) - this is the strategy now being used to contain the pandemic after the “lockdown” [1]. The Vienna University of Technology and its spin-off company dwh have now analysed to what extent the number of infections can be contained if efficient tracing is used consistently and even more than before.
The major goal is to keep the so-called reproduction number R permanently below one. This means that on average an infected person infects less than one other person. If this is successful, the disease figures will decrease - in contrast to the sharp increase that can be expected when R is above one.
However, the dynamics of the infections are not yet fully described by the reproduction number R. Their value currently varies greatly from region to region. The dispersion parameter is also important. A high dispersion factor means that many of the infected persons each infect a similar, relatively small number of other persons - the disease is thus spread in a fairly uniform manner. A low dispersion parameter means that many infected people do not infect anyone or very few people, while the majority of new infections are due to a few superspreaders, which are responsible for dozens or even hundreds of infections [2, 3].
Superspreader: Different scenarios
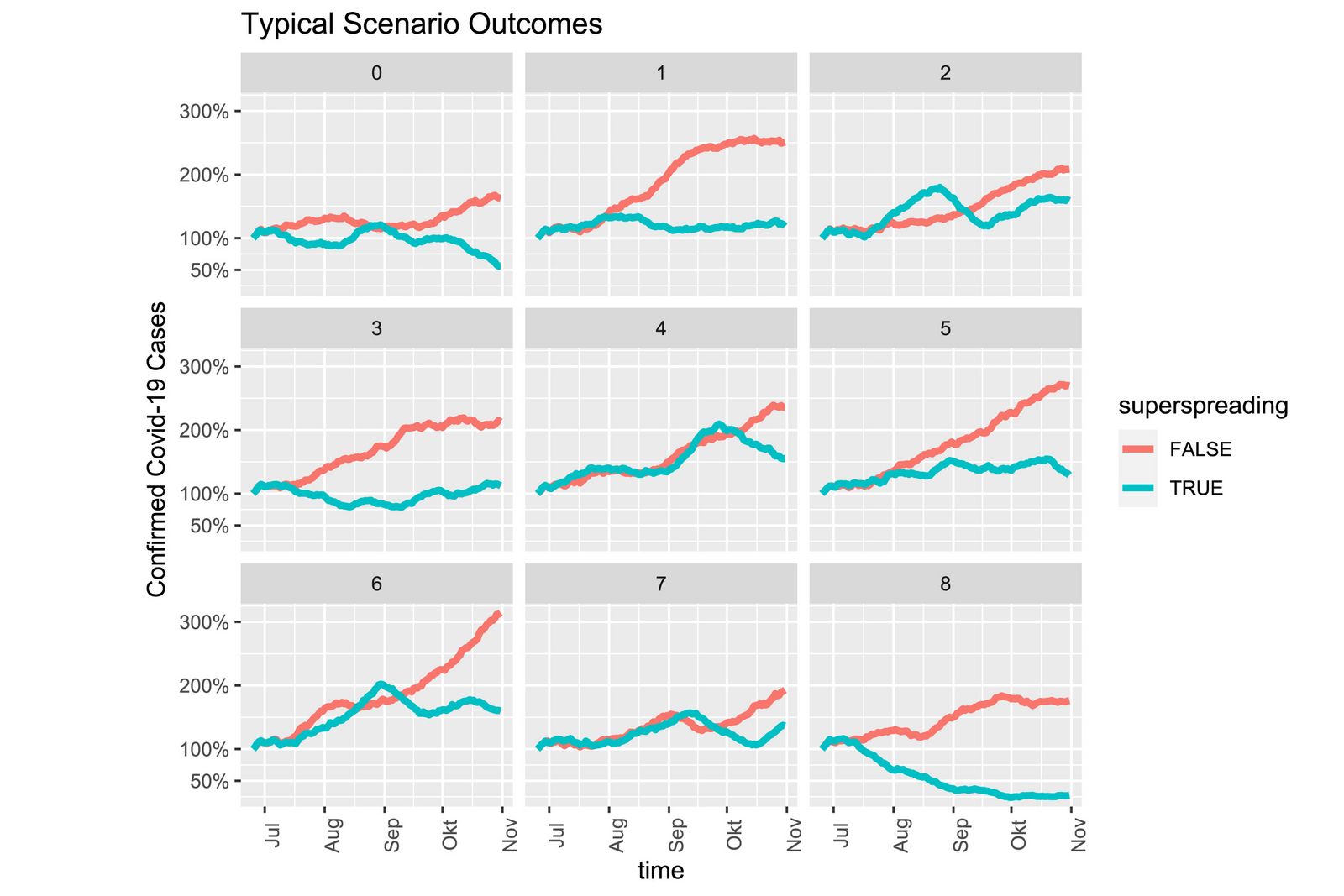
The research team, which under the leadership of Niki Popper has been simulating the spread of COVID-19 in agent-based computer models since the end of January, has now analysed how different dispersion factors affect the disease figures. The results show that if a large proportion of infections can be traced back to superspreaders, contact tracing becomes more efficient and the probability of being able to continue to contain the number of people who fall ill increases.
At this stage of the epidemic, however, it is not possible to make exact forecasts. Especially when the dispersion factor is small and the dynamics are determined by a few superspreaders, chance plays a major role. This randomness is reproduced in the computer model: Just like in reality, the events that lead to the spread of the disease occur purely by chance. However, the calculations can be repeated as often as required - each time with different random events. This process (also known as Monte Carlo simulation) gives a good picture of when and how often the epidemic takes what course. It is possible to calculate the probability that, as the number of cases increases, the measures (tracing and quarantine) will take effect sufficiently quickly to keep the pandemic under control.
The model
As a basis for the scenario calculations, a model specially developed for Austria (preprint available under [5]) was used and adapted. A very effective TTI strategy is assumed, i.e. people are very quickly removed from the dispersal networks. The following assumptions were made:
- Modelled tracing strategy: If a person tests positive for SARS-CoV-2, the remaining household members of the infected person are isolated on the same day (home quarantine) and within 36 hours the direct work colleagues as well as 75% of the potentially infectious leisure contacts are identified and also preventively isolated for 14 days.
- The previous relaxation measures (up to 1.7.) are depicted in the model. A further reduced contact behaviour in leisure time is taken into account (based on mobility data from mobile phone providers, which are integrated in the WWTF-funded project “Synthesis of disease spread and network data for the Covid-19 simulation”) and that the majority of leisure time contacts take place outdoors, i.e. with a lower risk of infection.
- The assumption on superspreading
- A) an assumed disease with high dispersion factor (approx. 0.8, hardly/no superspreader)
- B) low dispersion factor (many superspreaders, essentially corresponding to the estimate for COVID-19 from the literature, for example in [4])
- The simulations were started on 24.6. with daily updated data and information, therefore the absolute values are lower than the current figures.
This computer experiment is specifically concerned with the role of good tracing and isolation of potentially infected contact persons. Apart from the well-known fact that tracing slows down the spread, the results show that, thanks to a low dispersion factor, new clusters can be brought under control particularly well and a sharp increase in the epidemic curve can be avoided with a higher probability.
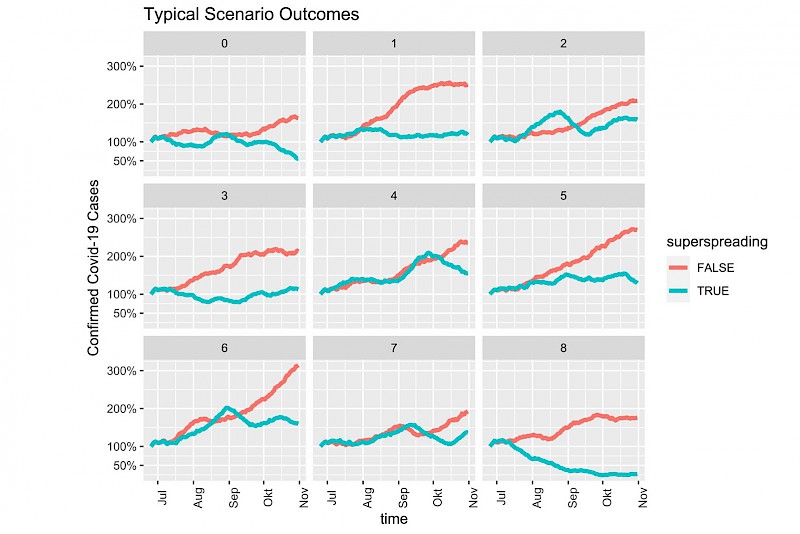
Assuming the current situation with currently valid precautions, local outbreaks are contained with over 90% probability by the very strong TTI strategy (testing, tracing, isolation) depicted in the model. If, on the other hand, the epidemic were to spread with a high dispersion factor, the epidemic curve would only be contained again in less than 35 % of cases using the same strategy. Tracing also has limits
For the future, one must also consider that tracing is only possible within certain limits: it requires human resources. The simulations assume that contact tracing of infected persons is still possible in all cases. “Our results show that efficient tracing is now crucial,” emphasizes Niki Popper. “However, this does not mean that you should simply use as many people as possible for contact tracing. It’s about quality: we need people who are also trained for it, who have the necessary resources and who follow a clear, sensible strategy”.
If the number of infected persons increases significantly or if particularly large clusters are formed, it could happen that the existing resources in the health care system are no longer sufficient for effective tracing. This possibility is not considered in the model. In addition, the model currently assumes that leisure time behaviour will remain the same - this must also be reconsidered when making forecasts for the autumn, when contacts will again increasingly take place indoors.
References
[1] A. J. Kucharski u. a., „Effectiveness of isolation, testing, contact tracing, and physical distancing on reducing transmission of SARS-CoV-2 in different settings: a mathematical modelling study“, The Lancet Infectious Diseases, S. S1473309920304576, Juni 2020, doi: 10.1016/S1473-3099(20)30457-6.
[2] J. O. Lloyd-Smith, S. J. Schreiber, P. E. Kopp, und W. M. Getz, „Superspreading and the effect of individual variation on disease emergence“, Nature, Bd. 438, Nr. 7066, S. 355–359, Nov. 2005, doi: 10.1038/nature04153.
[3] B. M. Althouse u. a., „Stochasticity and heterogeneity in the transmission dynamics of SARS-CoV-2“, arXiv:2005.13689 [physics, q-bio], Mai 2020, Zugegriffen: Juni 16, 2020. [Online]. Verfügbar unter: http://arxiv.org/abs/2005.13689.
[4] B. M. Althouse u. a., „Stochasticity and heterogeneity in the transmission dynamics of SARS-CoV-2“, arXiv:2005.13689 [physics, q-bio], Mai 2020, Zugegriffen: Juni 16, 2020. [Online]. Verfügbar unter: http://arxiv.org/abs/2005.13689.
[5] M. R. Bicher, C. Rippinger, C. Urach, D. Brunmeir, U. Siebert, und N. Popper, „Agent-Based Simulation for Evaluation of Contact-Tracing Policies Against the Spread of SARS-CoV-2“, Epidemiology, preprint, Mai 2020. doi: 10.1101/2020.05.12.20098970.
Translation by DeepL, author of original Version: Florian Aigner, TU Wien